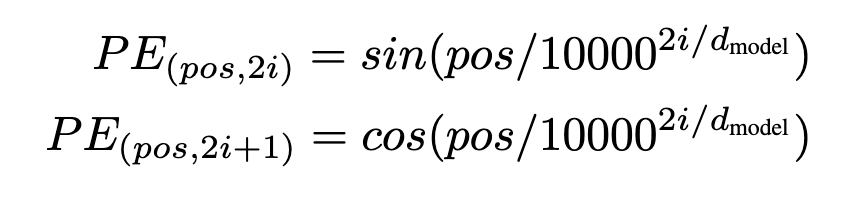Analyzing the Transformer Model Research Paper
Attention Is All You Need - Transformer Model
Sources:
These are my notes from reading the published paper on the Transformer Model from 2017. This research paper was published by Google researchers that created the transformer architecture that drastically revolutionized NLP and created the basis for LLMs. This architecture replaced traditional Recurrent Neural Networks (RNNs) and Convolutional Neural Networks (CNNs) by focusing on an attention-based mechanism.
The General Description is transcribed from Andrew Ng’s Generative AI with LLMs while the detailed notes are my own thought while reading through the actual research paper. Bullets with quotation marks represent my personal thoughts and tips for better understanding how the model works.
General Description:
By using self-attention to compute representations of input sequences, the model can capture long-term dependencies and parallelize computation effectively. It consists of an encoder and a decoder layer, each of which contain multiple layers. Within each layer, there are two sub-layers that include a multi-head self-attention mechanism and a feed-forward neural network. Multi-head self attention allows the model to attend to different parts of the input sequence, the feed-forward network applies a point-wise fully connected layer to each position separately and identically. It also uses residual connections and layer normalization to facilitate training and prevent overfitting while introducing a positional encoding scheme that encodes the position of each token in the input sequence. This enables the model to capture the order of the sequence without the need for recurrent or convolutional operations.
Detailed Notes:
Abstract
- New network architecture, the Transformer, based on attention mechanisms.
Introduction
- Recurrent models factor computation along the symbol positions of the input and output sequences.
- Generates a sequence of hidden states \(h_t\), as a function of the previous hidden state \(h_{t-1}\) and the input for position t
- Sequential nature does not allow for parallelization with training examples
- “Think parallel compute of pandas vs pyspark”
- Propose the Transformer, that relies entirely on attention mechanism to draw global dependencies between input and output
- avoiding recurrence and allows for parallelization
Background
- Goal of reducing sequential computation forms foundation of Extended Neural GPU, ByteNet, and ConvS2S, which use convolutional neural networks
- computing hidden representations in parallel for all input and output positions
- number of operations required to relate signals from two arbitrary input or output positions grows in the distance between positions
- linearly for ConvS2S and logarithmically for ByteBet
- makes it hard to learn dependencies between distant positions
- The transformer reduces this to a constant number of operations
- at the cost of reduced effective resolution
- due to averaging attention-weighted positions
- this is counteracted with the Multi-Head Attention
- at the cost of reduced effective resolution
- Self-attention (intra-attention) relates different positions of a single sequence to compute a representation of the sequence
- end-to-end memory networks are based on recurrent attention instead of sequence-aligned recurrence
- Transformer is first transduction model relying on self-attention to compute representations of its input and output without sequence-aligned RNNs or convolution
- “transduction (or transductive inference) - reasoning from observed, specific (training) cases to specific (test) cases”
- “contrary to induction - reasoning from observed training cases to general rules, which are then applied to test cases”
- “transductive is similar to semi-supervised learning, it’s using all input despite if it is known or unknown”
- pros: can make better predictions with fewer labeled points - (ex: it uses the unknown classified points to create clusters then assigns using the few labeled points)
- cons: no predictive abilities, needs to be repeated if new point is added and can be computationally expensive vs a supervised learning algorithm can label new points instantly with minimal computation
- “Link: Transduction Wikipedia "
Model Architecture
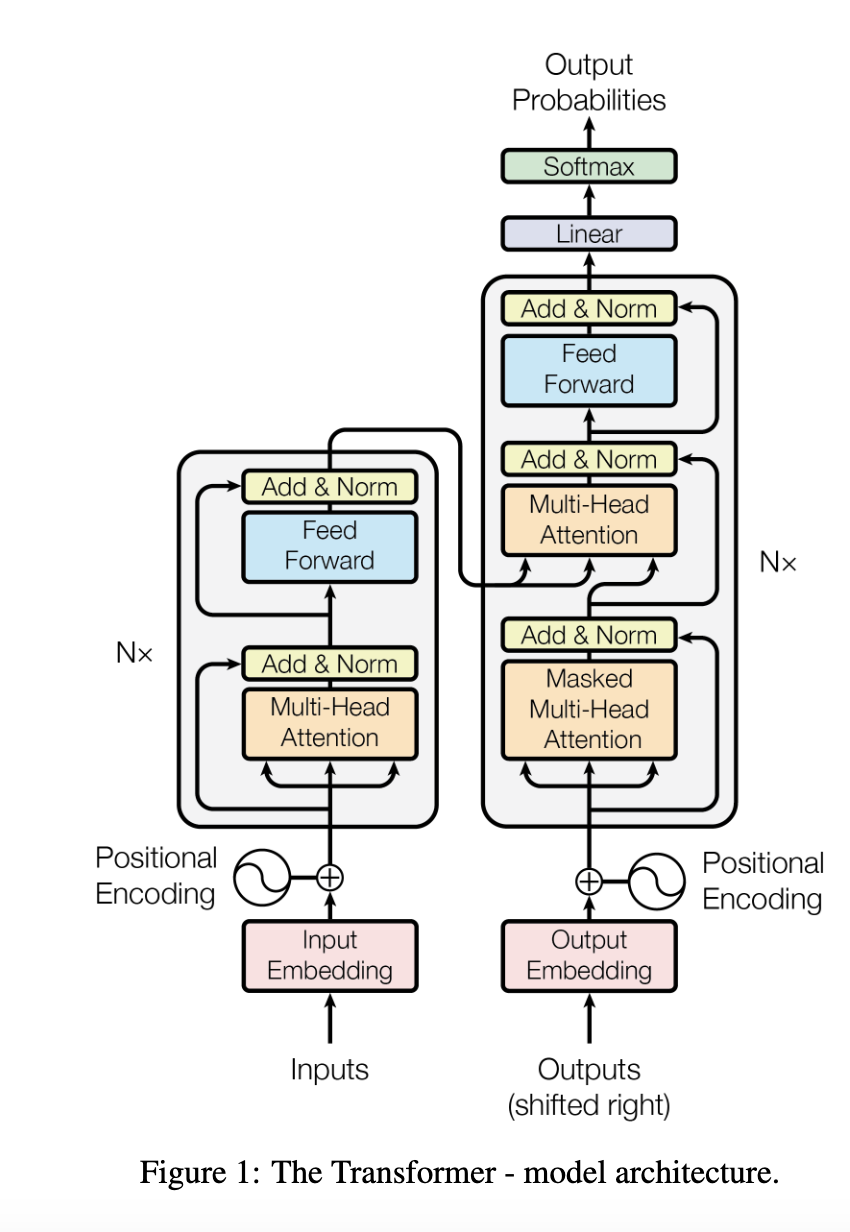
- Most competitive neural sequence transduction models have an encoder-decoder structure
- in this case, encoder maps an input sequence of symbol representations \((x_1, …, x_n)\) to a sequence of continuous representations \((z_1, …, z_n)\)
- given z, decoder generates an output sequence \((y_1, …, y_m)\) of symbols one element at a time
- at each step the model is auto-regressive
- meaning it consumes the previously created symbols as additional input when generating the next
- The Transformer follows this architecture
- uses stacked self-attention and point-wise connected layers
- Encoder is on left of above image, Decoder is on right
- Notice how Encoder output goes into Decoder midway through, as Decoder must incorporate the past generated outputs
Encoder
- stack of N=6 identical layers
- each has 2 sublayers
- first is a multi-head self-attention mechanism
- second is a simple position-wise fully connected feed-forward network
- Employ a residual connection around each of the two sub-layers
- layer is normalized
- output of each sub-layer is LayerNorm(x + Sublayer(x))
- sublayer(x) = function implemented by the sub-layer itself
- output of each sub-layer is LayerNorm(x + Sublayer(x))
- all sub-layers as well as the embedding layers produce outputs of dimension d=512
- each has 2 sublayers
Decoder
- stack of N=6 identical layers
- decoder inserts a third sub-layer in addition to the sub-layers each in each encoder layer
- performs multi-head attention over the output of the encoder stack
- “So it is analyzing its own output, then adds in the output of the encoder”
- employ residual connection around each of the sub-layers
- followed by layer normalization
- modify the self-attention sub-layer in the decoder stack to prevent positions from attending to subsequent positions
- This is masking, also note that the output embeddings are offset by one position
- this ensures the predictions of position i can only depend on the known outputs at positions less than i
- “only looking at past predictions, not current symbol prediction”
- decoder inserts a third sub-layer in addition to the sub-layers each in each encoder layer
Attention
- attention function: mapping a query and a set of key-value pairs to an output
- where the query, keys, values, and output are all vectors
- the output is computed as a weighted sum of the values
- where weight assigned to each value is computed by a compatibility function of the query with the corresponding key
- where weight assigned to each value is computed by a compatibility function of the query with the corresponding key
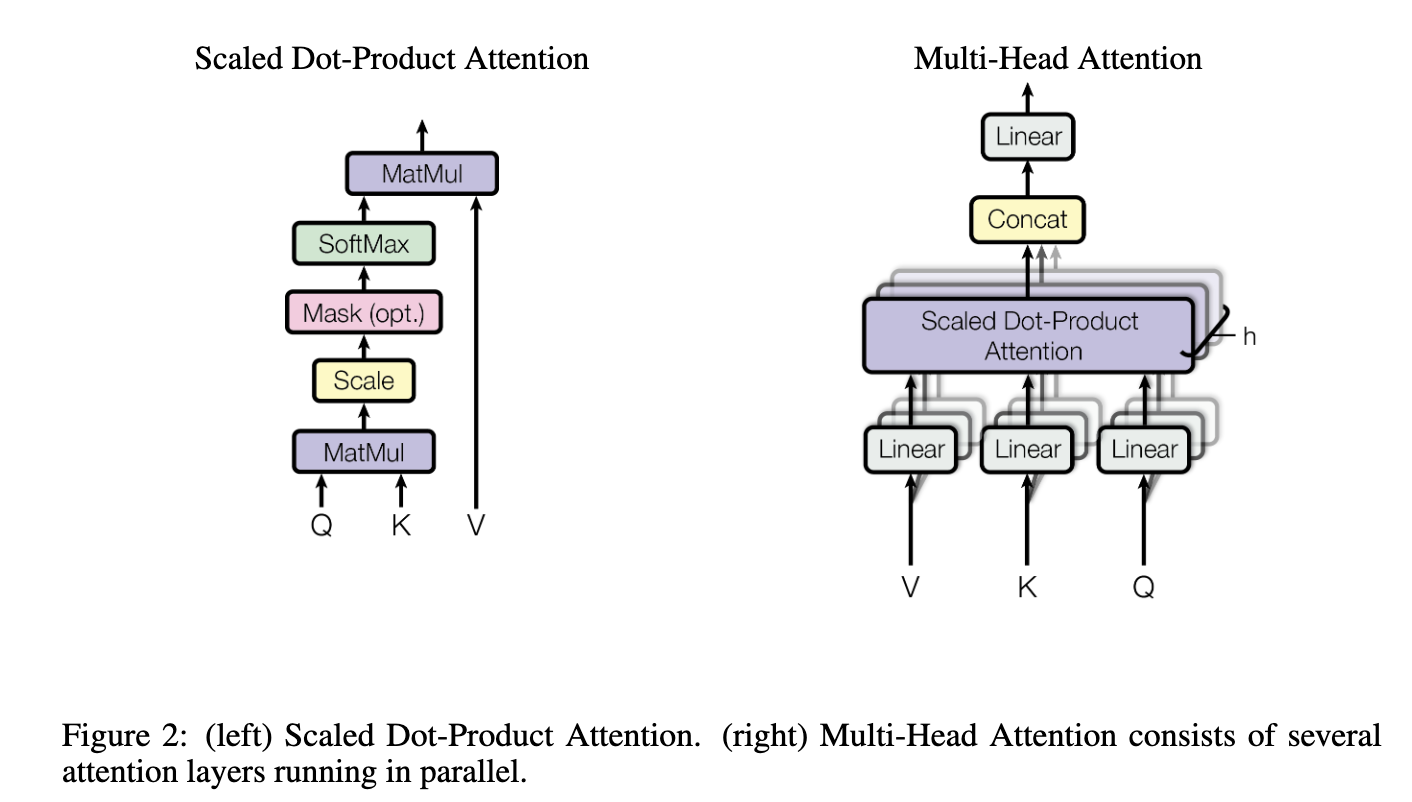
Scaled Dot-Product Attention
- Inputs consist of queries and keys of dimension \(d_k\), and values of dimension \(d_v\)
- To obtain the weights on the values:
- Dot product of the query with all keys
- divide each by \(\sqrt{d_k}\)
- and apply a soft max function
- To obtain the weights on the values:
- The attention function is computed on a set of queries simultaneously (matrix Q)
- Keys and values are in matrices K and V
- Gives us the matrix of outputs as:
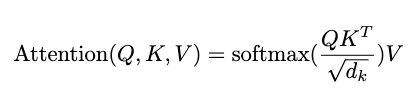
- “Look at this equation and the graphic for Scaled Dot-Product Attention”
- In the first step, MatMul is the same as our Dot-Product of Q and K transpose
- Second step, scale using the \(\frac{1}{\sqrt{d_k}}\)
- Third step SoftMax function on that output (skipped the optional masking)
- Finally fourth step is taking that output and multiplying by the V Matrix
- “Look at this equation and the graphic for Scaled Dot-Product Attention”
- Two most common attention functions are additive attention and dot-product attention
- Transformer is identical to dot-product attention except for the scaling factor of \(\frac{1}{\sqrt{d_k}}\)
- Additive attention computes the compatibility function using a feed-forward network with a single hidden layer
- Dot-product is much faster and more space-efficient than additive by using highly optimized matrix multiplication code
- Similar in theoretical complexity but not in speed or space
- “leveraging Linear Algebra and Matrices - basic example of why matrices are faster is matrix multiplication is a single operation to solve a system of linear equations, vs solving each individual equation”
- Scaling the dot products by \(\frac{1}{\sqrt{d_k}}\) counteracts large values of \(d_k\)
- The dot products grow large in magnitude and softmax will end up in regions with very small gradients
- EX: assume the components of q and k are independent random variables with mean 0 and variance 1
- Their dot product -
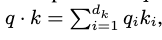
- has mean of 0 but variance of \(d_k\)
- Their dot product -
- “Softmax is a form of logistic regression (called multi-class logistic regression)"
- Turns a vector of K real values into a vector of K real values that sum to 1
- Makes them be able to be interpreted as probabilities
- Remember, softmax is exponential so larger numbers are weighted much more heavily
Multi-Head Attention
- Instead of a single attention function with \(d_{model}\)-dimensional keys (K), values (V) and queries (Q), they linearly project them h times with different learned linear projects
- The attention function is performed in parallel on each of these projected versions of Q, K, and V
- Yielding in \(d_v\)-dimensional output values
- Output values are concatenated and once again projected resulting in the final values
- The attention function is performed in parallel on each of these projected versions of Q, K, and V
- Allows for the model to jointly attend to information from different representation subspaces at different positions
- In a single attention head, averaging inhibits this
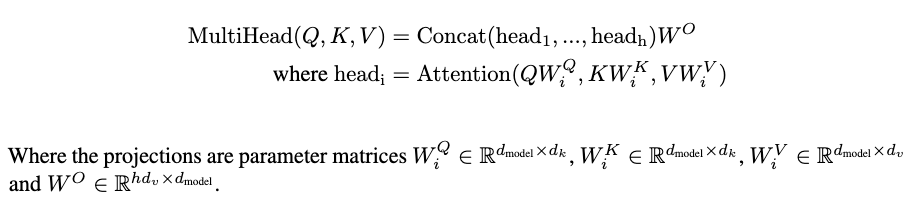
- In a single attention head, averaging inhibits this
- They used an h = 8 parallel attention layers, (or heads)
- For each of these layers they had \(d_k=d_v=\frac{d_{model}}{h}=64\)
- The reduced dimensions of each head made the total computational cost similar to a single-head attention with full dimensionality
- “The W matrices are simply the linear projection parameters used to create the correct dimensions to compute attention”
- “This reduces the dimension of each head and thereby reduces the total computational cost to be similar to single-head attention that has not been reduced”
Applications of Attention in The Model The Transformer uses multi-head attention in three different ways:
- encoder-decoder attention layers
- queries are coming from the previous decoder layer while the memory keys and values come from the output of the encoder
- every position in the decoder attends all positions in the input sequence
- mimics typical encoder-decoder attention mechanisms in sequence-to-sequence models
- “So here, we are forcing the decoder to ALWAYS look at the input”
- encoder self-attention layers
- In the self-attention layer all the keys, values and queries come from the output of the previous layer in the encoder
- each position in the encoder can attend to all positions in the previous layer of the encoder
- decoder self-attention layers
- allows each position in the decoder to attend to all positions in the decoder up to and including that position
- need to prevent leftward information flow in the decoder to preserve the auto-regressive property
- implemented inside of scaled dot-product attention by masking all values in the input of the softmax to illegal connections aka −∞
- “setting to negative infinity forces it to not look at subsequent values”
- “language is written left to right, so you can’t ‘peak’ ahead”
- implemented inside of scaled dot-product attention by masking all values in the input of the softmax to illegal connections aka −∞
Position-wise Feed-Forward Networks
- each layer in the encoder and decoder also contains a fully connected feed-forward network
- applied to each position separately and identically
- consists of two linear transformations with a ReLU activation in between
- “ReLU activation function for NN - https://en.wikipedia.org/wiki/Rectifier_(neural_networks)"
- “Basic ReLU essentially is taking the positive part of tits argument - i.e. f(x) = max(0,x)”
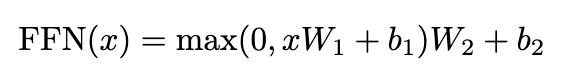
- “So we are taking ReLU activation of linearly transformed x, then applying another linear transformation”
- consists of two linear transformations with a ReLU activation in between
- The linear transformations are the same across different positions
- but different parameters from layer to layer
- Another way of describing this is two convolutions with a kernel size of 1
- dimensionality of input and output is \(d_{model}\) = 512
- inner-layer has dimensionality of d(ff) = 2048
Embeddings and Softmax
- learned embeddings are used to convert the input tokens and output tokens to vectors of dimension \(d_{model}\)
- learned linear transformation and soft max function are used to convert the decoder output to predicted next-token probabilities
- In this model, the weight matrix between the two embedding layers and the pre-softmax linear transformation are the same
- in the embedding layers, those weights are multiplied by \(\sqrt{d_{model}}\)
Positional Encoding
- with no recurrence or convolution, the model still needs to make use of order of the sequence
- information on the relative or absolute position of the tokens are injected using ‘positional encodings’
- these are added to the input embeddings at the bottoms of the encoder and decoder stacks (see figure 1)
- same dimension \(d_{model}\) as the embeddings so they can be summed
- many choices of positional encodings, learned and fixed
- in this paper, sine and cosine functions of different frequencies are used:
- pos is the position and i is the dimension
- each dimension of the positional encoding corresponds to a sinusoid
- WHY? the wavelengths in these functions form a geometric progression from 2pi to 10000*2pi
- for any offset of k (so \(PE_{pos+k}\)) can be represented as a linear function of \(PE_{pos}\)
- “because we use sine/cos, you can end up at the same value by adding a linear value to it. think sin(0) = sin(2*pi) "
Why Self-Attention
- Total computational complexity per layer
- amount of computation that can be parallelized (minimum number of sequential operations required)
- path length between long-range dependencies in the network
- shorter the paths forward and backward signals must traverse between any combination of positions in the input and output sequences, the easier to learn long-range dependencies
Conclusion:
There is more information on the Training and Results of the model developed however this post is mainly to summarize what is happening from a mathematical and logical standpoint rather than the details of the specific model outlined in the research paper. This model can be adapted and changed with the number of layers, encoding structure, etc. however if you want to investigate the results of the research paper, I recommend you check out the link at the top of the post.